Basic Ratio Capacity May Serve as Building Block for Math Knowledge

Understanding fractions is a critical mathematical ability, and yet it’s one that continues to confound a lot of people well into adulthood. New research finds evidence for an innate ratio processing ability that may play a role in determining our aptitude for understanding fractions and other formal mathematical concepts.

The research is published in Psychological Science, a journal of the Association for Psychological Science.

“Our findings suggest that human beings come wired with a sort of naïve nonsymbolic ratio processing ability and that differences in these abilities have meaningful effects on the development of mathematical thinking,” explains psychological scientist Percival Matthews of the University of Wisconsin-Madison, lead researcher on the study. “This basic perceptual ability seems to have consequences even for complex mathematical thinking like algebraic reasoning, which is quite counterintuitive.”

Matthews and colleagues Mark Rose Lewis and Edward M. Hubbard, all of the University of Wisconsin-Madison, hypothesized that we must have some basic ability that allows us to reason, in an informal way, about proportions.

“The human brain existed way before we had things like math and reading, which means that however we do these things, we have to sort of recycle abilities that the brain already has,” Matthews explains.

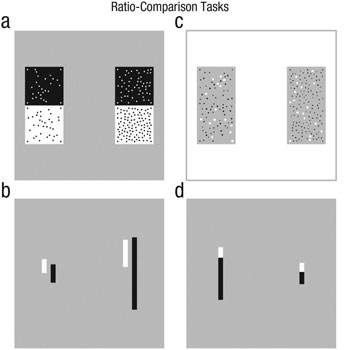
Sample dot and line pairs

To investigate this hypothesis, the researchers recruited 181 college undergraduates to participate in their study. The students completed four tasks in which they had to compare ratio quantities represented by pairs of dot arrays or pairs of line segments.

Students saw a pair of dot groupings or a pair of line segments on a computer screen for 1.5 seconds, and were asked to indicate which option in the pair represented a larger quantity. In making this assessment, the students essentially had to intuitively “feel out” and compare ratios composed by dot (or line) pairs on one side versus dot (or line) pairs on the other side.

Importantly, the ratios represented by the dots and the lines varied from trial to trial.

The students completed several additional tasks that gauged their formal, or symbolic, math ability.

In one task, they were presented a paper-and-pencil assessment of general fractions knowledge. In another, they were given a fraction – such as 1/7 – and were asked to represent the fraction by clicking on the analogous position on a number line that ranged from 0 to 1. The researchers also examined students’ scores on the algebra placement test that they took when they entered university.

The results revealed an association between the students’ ability to gauge nonsymbolic ratios and their competence in symbolic math: Students who were adept at processing pictorial ratios by comparing dots and lines also tended to be good at comparing fractions and estimating fractions on a number line.

But the association also extended to more general math skills: Students who scored higher on the pictorial ratios task also tended to be good at solving algebraic equations.

“Far and away the most surprising finding was that this ratio sensitivity was correlated with performance on university entrance exams,” says Matthews. “It is easy to see how sensitivity for the magnitudes of what amount to nonsymbolic versions of fractions might be correlated with fractions processing performance. However, it’s another thing for it to be correlated with something as complex as algebra.”

Matthews and colleagues are hoping to find evidence-based strategies that will make teaching and learning fractions more manageable, given the difficulty that many people have in mastering fractions. These new findings, they argue, serve as an important for step in that endeavor:

“At the end of the day, we want to encourage psychologists, math education researchers, and educational practitioners to consider how actively trying to leverage these abilities might help improve fractions learning,” says Matthews.

This research was supported in part by grants from the Wisconsin Alumni Research Fund and National Science Foundation Grant No. DRL-1420211.