The Minimum Description Length Principle

Both as scientists and in our everyday lives, we make probabilistic inferences. Mathematicians may deduce their conclusions from their stated premises, but the rest of us induce our conclusions from data. As scientists, we do so by examining the extent to which our hypotheses — the conclusions we might draw — explain or predict the data. One problem we face in doing so is that some hypotheses are more complex than others. A colleague once remarked about a conspicuously complicated theory that it was the only theory he knew that was harder to remember than the results it explained. How can we decide when complex hypotheses are justified?

Occam’s Razor (also known as the “law of parsimony”) has been recognized as an aspect of scientific thinking since Pythagoras (6th century BC). The principle counsels that when several theories explain the same data, the simplest one is preferable. But how do we measure simplicity? Does it live, like beauty, only in the eye of the beholder? And how can we measure how accurately competing theories explain the data? What do we do when the more complex theory more accurately describes the data, as is often the case? And how can we weigh its greater complexity (bad) against the accuracy with which it represents the data (good)?

In recent years, progress has been made on this question in inferential statistics, where hypotheses take the form of stochastic models; for example, Hypothesis 1 states that the data come from a normal distribution, whereas Hypothesis 2 states that they come from a Weibull distribution; or, Hypothesis 1 states that the data obey a power law, whereas Hypothesis 2 states that they obey a logarithmic law. Are these equally simple hypotheses? There are various ways of addressing that question, but the one that is arguably the simplest conceptually, the most applicable to modest data sets, and the most philosophically interesting is the minimum description length principle, which was worked out by Jorma Rissanen beginning in the late 1970s (Rissanen 1978, 1999; for tutorial, see Grünwald, 2005). It enables us to order stochastic models by an objective measure of their complexity, and it tells us how to resolve the trade-off between complexity and explanatory adequacy.

The idea is simplicity itself: The more wiggle room a stochastic model has, the more complex it is. This wiggle room can be measured by how accurately a model fits random data sets of a given size. Models with lots of wiggle room will fit many different such data sets fairly well; models with little wiggle room will fit fewer of them well. As explained in my first column on Bayes for Beginners, the likelihood of a model, given data, is the product of the probabilities the model assigns to those data. If there are three data points and the model assigns probability .5 to one, .2 to the second, and .3 to the third, then the likelihood of the model given those data is .5 x .2 x .3 = .03. The maximum likelihood for a model form is the likelihood you get when you adjust the parameters of the model to maximize that product. Generally speaking, the likelihood-maximizing parameter values for simple stochastic models are easily calculated.

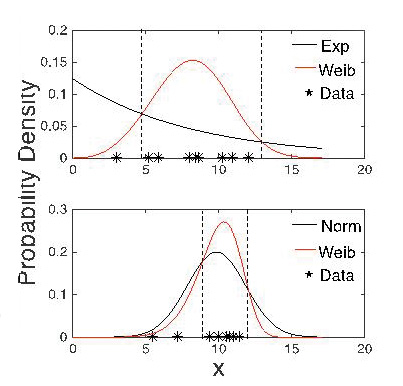Figure 1 illustrates the problem of model complexity and the likelihood measure of model fit. In making the figure, I drew 100 random samples of size 10 from an exponential distribution with a mean of 10, another 100 samples of that size from a normal distribution with the same mean and with a standard deviation of 2, and yet another 100 samples of that size from a Weibull distribution with a location parameter of 10 and a shape parameter of 1. (The Weibull distribution often is used to describe reaction-time data, which are usually left-skewed.) I then found the maximum likelihood fit for all three distributional forms to the three sets of 100 samples, and I compared the maximum likelihoods. The Weibull likelihood was a better fit than the exponential likelihood on every exponential sample, and the normal likelihood was a better fit than the exponential likelihood on 98% of the samples. Although the samples came from an exponential distribution, the Weibull and the normal distributional forms almost always described the data more accurately. The top panel shows an example of the Weibull distribution fitting the exponential data better than the exponential distribution.

Any statistician would say, “But of course! The normal and the Weibull have two free parameters, whereas the exponential has only one. Models with more free parameters generally fit data better.” Von Neumann is claimed to have said, “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” The number of parameters is not the whole story, however, because the Weibull distribution also beat out the normal distribution almost half the time. Both distributional forms have two parameters, but when both were fit to data drawn from a normal distribution, the Weibull distribution gave a better fit almost half the time. The bottom panel of the figure shows an example of the Weibull distribution fitting normal data better than the normal distribution does. It fits better because it can skew either left or right, whereas the normal is always symmetrical. The data in a small sample from a normal distribution often are slightly skewed by small-sample error.

We know from a famous theorem by Claude Shannon, the father of information theory, that there is a 1:1 mapping between the relative frequency of a datum from a given source (its probability) and the length of the code word one must assign to that datum in order to obtain the most efficient coding of the data from that source. The higher the probability of a datum, the shorter the code for it must be. Samuel Morse understood this intuitively when he made the dot the symbol for “e.” The dot is the shortest symbol in Morse code, and “e” is the most frequent letter in English words (e.g., the letter with the highest probability). If you are going to use a symbol frequently, you want it to be short; if a symbol is used infrequently, then it doesn’t matter if it’s long. This principle is the basis for modern data-compression schemes (.jpg, .mov, etc.). Such schemes make it possible to fit a large amount of data into a given amount of memory by using short codes for frequent data and long codes for infrequent data.

Rissanen’s minimum description length principle is this: A good model compresses data by telling us how long the code word should be for each datum; the higher the probability the model assigns to a datum, the shorter the code word for that datum should be. A corollary is that the more accurate a model is, the more it is able to compress the data. However, because the best compression scheme is determined by the data, we must encode the model itself into memory along with the data that we have encoded using it. If we don’t put the model in memory, we won’t know how to decode (uncompress) the data. Rissanen showed that we can measure the cost (in bits) of encoding the model for a given amount of data by computing the sum of its maximum likelihood fits to all possible data sets of that size. One naturally wonders whether that sum can be computationally approximated; it turns out that it often can. Thus, we can measure model-encoding cost and data-encoding cost with the same language-independent currency.

The principle links the resolution of the trade-off between model complexity and descriptive adequacy to the problem of finding the most efficient use of memory. The best model is the one that minimizes the amount of memory required to encode the data and the one that enables us to compress the encoding of the data. When one has little data, the cost of a complex model outweighs the additional data compression that it makes possible. However, it turns out that the model cost grows only as the logarithm of the amount of data, whereas the cost of encoding the data grows linearly. When we use a better model — one that captures real structure in the data — the data-encoding cost grows more slowly than when we use a poorer model. Thus, in the long run, the total memory load incurred using a more complex model (e.g., the Weibull rather than the normal) will be smaller than the load incurred by using a simpler model if and only if the more complex model captures genuine structure in the data (rather than small-sample error). When we have only a little data, the principle favors simpler models. As we acquire more data, it will favor a more complex model only if it pays for its complexity with increased memory savings.

The most exciting thing about this principle is that it means that, under reasonable conditions, the model that makes the most efficient use of memory given the data we already have does the best job of predicting the data not yet seen. Thus, a stochastic model with just the right complexity does two things: It minimizes memory load and it maximizes predictive accuracy. My colleague was right to stress the fact that the complex theory was harder to remember than the results it explained. œ

References

Grünwald, P. D. (2004). A tutorial introduction to the minimum description length principle. In P. D. Grünwald, J. I. Myung, & M. A. Pitt (Eds.), Minimum description length: Theory and applications (pp. 23–81). Cambridge, MA: MIT Press.

Rissanen, J. (1978). Modeling by shortest data description. Automatica, 14, 465–471.

Rissanen, J. (1999). Hypothesis selection and testing by the MDL principle. The Computer Journal, 42, 260–269.