There’s Life Beyond .05

As part of a comprehensive effort to promote sound research practices in psychological science, the field’s leading journal has introduced new innovative guidelines for authors submitting articles on their findings.

The new guidelines for Psychological Science are aimed at enhancing the reporting of research methods and promoting robust research practices, says Editor in Chief Eric Eich of the University of British Columbia. Submitting authors are now required to state that they have disclosed all important methodological details, including excluded variables and additional manipulations and measures, as a way of encouraging methodological transparency.

To help fuel the robustness of the science, the journal has been inviting authors to use the “new statistics” of effect sizes, confidence intervals, and meta-analyses in an effort to avoid problems typically associated with null-hypothesis significance testing (NHST). The journal has published a statistics tutorial by Geoff Cumming of La Trobe University in Australia. “The New Statistics: Why and How” is freely available online. Here, Cumming explains in detail the “new statistics” approach, the focus of ongoing discussion about data analysis.

In the 1950s, psychology started adopting null-hypothesis significance testing (NHST), probably because it seemed to offer a scientific, objective way to draw conclusions from data. NHST caught on in a big way and now almost all empirical research is guided by p values — which are in fact tricky conditional probabilities that few understand correctly.

Why did NHST become so deeply entrenched? I suspect it’s the seductive but misleading hints of importance and certainty — even truth — in a statement that we’ve found a “statistically significant effect.” NHST decisions can be wrong, and every decent textbook warns that a statistically significant effect may be tiny and trivial. But we so yearn for certainty that we take statistical significance as pretty close.

For more than 50 years, however, leading scholars — Paul Meehl, Jacob Cohen, and many others — have explained the deep flaws of NHST and described how it damages research progress. Most reformers have advocated estimation — meaning effect sizes and confidence intervals (CIs) — as a much more informative way to analyze data.

Cohen famously said that he suspected “the main reason they [CIs] are not reported is that they are so embarrassingly large.” Yes, it’s discouraging to report that the average improvement in response time was 34 ms, 95% CI [7, 61], which means the true improvement could plausibly be anywhere between 7 ms and 61 ms. But the CI gives accurate information about uncertainty, and we need to come to terms with that — it’s way more informative than a mere claim of a statistically significant improvement.

NHST was under attack in other disciplines, also. Prompted by epidemiologist Ken Rothman and others, medicine in the 1980s started expecting CIs to be routinely reported. Since then most empirical articles in medicine have reported CIs, although interpretation is still usually based on NHST.

In 1990 Rothman founded the journal Epidemiology, stating that it would not publish NHST. For the decade of his editorship, it flourished and published no p values, demonstrating that successful science does not require NHST. In psychology, APS Fellow Geoff Loftus edited Memory & Cognition from 1993 to 1997 and strongly encouraged figures with error bars — such as CIs — instead of NHST. He achieved some success, but subsequent editors returned to NHST business as usual.

Psychology and other disciplines using NHST were in a strange situation. NHST was repeatedly demonstrated to be deeply flawed: Almost no defenses of it were published, and yet it persisted. Pioneering editors like Rothman and Loftus could rattle the cage, but couldn’t set their disciplines free of the p value. Statistics teaching, textbooks, software, the APA Publication Manual, journal guidelines, and universal practice all largely centered on NHST. We claimed to be a science, but could not change our methods in the face of evidence and cogent argument that there are vastly better ways.

Meanwhile, meta-analysis was becoming widely used. Meta-analysis requires estimation information from all studies, and p values are irrelevant. Many hoped that the rise of meta-analysis might give us collective insight and loosen the hold of NHST. But it didn’t.

Then came reports that some well-accepted results could not be replicated. From cancer research to social psychology, it seemed that an unknown proportion of results published in good journals were simply incorrect. This was devastating — which scientific results could we trust?

In 2005, Stanford University Professor of Medicine John Ioannidis connected the dots in a famous article titled “Why Most Published Research Findings Are False.” He identified the overwhelming imperative to achieve statistical significance as a core problem. It was imperative because it was the key to publication, and thus to jobs and funding. It had three terrible effects. First, it led to selective publication — journals rarely found space for results not reaching statistical significance. Therefore, second, researchers sought ways to select and tweak during data analysis, to find some result that could be declared statistically significant. Third, any result that once achieved p < .05 and was published was considered established, so replication was rare.

Ioannidis argued convincingly that the combination of these three effects of reliance on NHST may indeed have resulted in most published findings being false. Suddenly this was serious — the foundations of our science were creaking. Happily, a range of imaginative responses have now emerged and are developing fast — several are described elsewhere in this issue of the Observer.

Most excitingly, NHST was, at long last, subjected to renewed scrutiny. The 2010 edition of the APA Publication Manual included the unequivocal statement that researchers should “wherever possible, base discussion and interpretation of results on point and interval estimates.” It included for the first time numerous guidelines for reporting CIs.

I refer to effect sizes, CIs, and meta-analysis as “the new statistics.” The techniques themselves are not new, but using them would for many researchers be quite new, as well as a great step forward. My article in Psychological Science is intended to explain why we need to shift from NHST, and how in practice to use estimation — meaning the new statistics — in a range of common situations. There’s more in my book, Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis.

Beyond NHST, estimation is probably the most immediately usable strategy, but other valuable approaches, especially Bayesian techniques, should also flourish. Never again will anything, even CIs, be as universally relied on as the p value has been — and that’s great news!

Why should the bold policies of Psychological Science to improve research practices and embrace the new statistics be any more successful than past reform attempts? Here are just a few of the reasons for optimism:

• The replicability crisis and Ioannidis’s arguments are dramatically strong motivations — we simply must do better;
• There are many resources we can use right now to help us leave behind the security blanket of p;
• There are corresponding developments in other disciplines; and
• Editor in Chief Eric Eich and his editorial team are on the case.

There remain great challenges: We need better textbooks, better statistics courses, much better software, and more examples of good practice. But these are coming. If I ever need to be reminded that we’re on the right track, I consider the dance of the p values, which illustrates how unreliable any p value is. It’s simply nuts to rely on p! œ

Confidence Intervals — Beautiful Pictures of Uncertainty

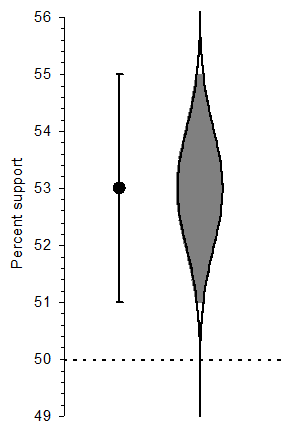
A 95% confidence interval marked by conventional error bars (left), and the beautiful cat’s eye shape of a CI (right).

You read that “a poll found support for the Prime Minister to be 53%, with a 2% margin of error.” The error bars at left in the figure show that range [51, 55], which is the 95% confidence interval (CI). We can say we are 95% confident the true population level of support for the Prime Minister lies in that interval. Values in the interval are plausible for the true level of support, and values outside the CI are relatively implausible.

A CI tells us much more than NHST, but we can use a CI to do NHST: Any value lying outside the CI is implausible as the true value and can be rejected. Because 50% lies outside the CI, we reject the hypothesis of 50% and conclude that support is statistically significantly greater than 50%. The further the CI from the null hypothesis value, the lower the p value. Our CI is sufficiently above 50% to give p < .01. But the best strategy is to focus on the CI and not think about NHST or p at all.

The cat’s eye picture at right in the figure shows how plausibility varies. The fatter the graphic, the more likely a value is the true level of support. Our best bet for the true value is around 52% to 54%, where the graphic is fattest, and plausibility or likelihood decreases smoothly for lower and higher values. See a CI and bring to mind the cat’s eye, which is a beautiful picture of the extent of uncertainty in our data.

 

References

American Psychological Association. (2010). Publication manual of the American Psychological Association (6th ed.). Washington, DC: American Psychological Association.

Cohen, J. (1994). The earth is round (p < .05). American Psychologist, 49, 997–1003.

Cumming, G. (2012). Understanding the new statistics: Effect sizes, confidence intervals, and meta-analysis. New York: Routledge.

Cumming, G. (2013). The new statistics: Why and how. Psychological Science, 27, 7–29. Retrieved from www.tiny.cc/tnswhyhow

Ioannidis, J. P. A. (2005). Why most published research findings are false. PLOS Medicine, 2, e124. doi: 10.1371/journal.pmed.0020124