Presidential Column
Bayes for Beginners 3: The Prior in Probabilistic Inference
In this, the final column in a series on Bayes for Beginners, C. Randy Gallistel explains the role of prior distributions in deciding between competing conclusions that might be drawn from experimental data. For more information, read Bayes for Beginners 1 and Bayes for Beginners 2.
 As explained in the preceding column, a prior is a probability distribution on the possible values of the parameters of a statistical model for one’s data. The prior distribution allows us to incorporate preexisting knowledge and beliefs into our prediction before we’ve analyzed our data. The Bayesian calculation multiplies a prior distribution by the likelihood function, point by corresponding point. The likelihood function, which was explained in the first column, depends only on the data. It expresses the uncertainty, given the data, about what the values of the model’s parameters could be. In Bayesian hypothesis testing, competing hypotheses are represented by competing prior distributions, which may be seen as competing “bets” on where the likelihood function will be high.
As explained in the preceding column, a prior is a probability distribution on the possible values of the parameters of a statistical model for one’s data. The prior distribution allows us to incorporate preexisting knowledge and beliefs into our prediction before we’ve analyzed our data. The Bayesian calculation multiplies a prior distribution by the likelihood function, point by corresponding point. The likelihood function, which was explained in the first column, depends only on the data. It expresses the uncertainty, given the data, about what the values of the model’s parameters could be. In Bayesian hypothesis testing, competing hypotheses are represented by competing prior distributions, which may be seen as competing “bets” on where the likelihood function will be high.
Suppose we test a subject on her ability to predict the outcomes of 10 successive tosses of a fair coin, and she makes 6 successful predictions. Two competing hypotheses we might entertain are: 1) that she was a bit lucky and that her true chance of successfully predicting these outcomes is .5, or 2) that she is clairvoyant and that her true chance of predicting these outcomes is greater than .5.
In the conventional (non-Bayesian) approach, we test only the first hypothesis (the null hypothesis). When it fails (when the result is “significant”), we conclude that the second hypothesis is probably true, even though we neither formulate it quantitatively nor test it. If the null hypothesis does not fail (p = n. s.), we conclude nothing, because we remember that insignificant p values cannot be offered in support of a null hypothesis (even though they frequently are so offered).
In the Bayesian conceptual framework, we formulate both hypotheses precisely and test both of them against the data. Our calculation delivers the “Bayes factor,” which tells us the extent to which the data weigh in favor of one hypothesis or the other.
We formulate our hypotheses as prior probability distributions. A hypothesis may be viewed as a bet on where the data will fall. To make these bets, we allot each of the hypotheses the same number of probability “chips.” These chips are the bits of probability in a probability distribution that always sum to 1. The probability chips of different hypotheses are distributed differently (upper panel of Figure 1 on the following page).
To understand Bayesian inference, it helps to plot the competing prior probability distributions and the likelihood function over their common axis — in this case, the possible values for p (see Fig. 1). When we multiply the different bits of probability in a prior by the likelihood function (the basic Bayesian computation), we determine the extent to which the likelihood favors each bit of probability in that prior. Chips placed where likelihood is high are good bets; chips placed where it is low are bad bets. The hypothesis favored by the data is the one whose chips (e.g., bits of probability) have the highest overall likelihood. The more unequal the relative “winnings,” the more the data weigh in favor of the winning hypothesis.
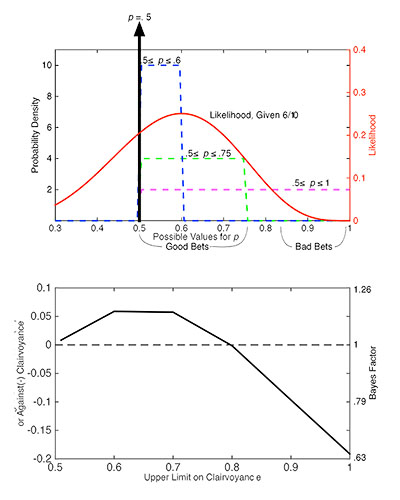
Figure 1. The upper panel plots the prior probability distributions representing several different hypotheses (against the left axis) and the likelihood function given 6 successful predictions of 10 flips (against the right axis), over their common axis (the possible values for the probability of a correct prediction). To determine how the data weigh, we multiply each bit of probability in a given prior probability distribution by the corresponding value of the likelihood function. Those bits that correspond to high likelihood are well-placed bets; those that correspond to low likelihood are badly placed bets. The overall likelihood of a hypothesis is the sum of the products. The lower panel plots the weight of the evidence in favor of clairvoyance (vs. chance) as a function of how strongly we hedge the clairvoyance hypothesis (the maximum predicted effect size). As we reduce the upper limit on the possible degree of clairvoyance to .5, the clairvoyance hypothesis becomes indistinguishable from the null hypothesis.
Betting on the simplest form of the clairvoyance hypothesis means spreading our chips evenly over the above-chance half of the p axis (magenta distribution in Fig. 1), whereas betting on the null hypothesis means putting all of our chips at .5 (vertical heavy black arrow). To embrace more hedged forms of the clairvoyance hypothesis, we reduce the maximum hypothesized effect size. One might argue that no subject is unfailingly clairvoyant — so it is unreasonable to put clairvoyance chips above, say, p = .75 (the green distribution) — or even that subjects can only be expected to be at most a little bit clairvoyant — so that it is unreasonable to put clairvoyance chips above p = .6 (the blue distribution). Note that in going from the simple form of the clairvoyance hypothesis (magenta) to the hedged forms (green and blue), we move chips that were in a bad-bet region into a good-bet region, which is why hedging the clairvoyance hypothesis improves its likelihood.
Rather than ponder what an appropriate degree of hedging for the clairvoyance hypothesis might be, it is instructive to compute the “weight of the evidence” (common logarithm of the Bayes factor) as a function of the degree of hedging (lower panel of Fig. 1). Taking the logarithm of the Bayes factor converts Bayes factors < 1 (those favoring the null) into negative numbers, and it equates negative and positive odds, so that equal distances from weight 0 (the horizontal dashed line) represent equal degrees of favor for one hypothesis or the other.
We see from the plot in the lower panel that no matter how we hedge the clairvoyance hypothesis, these data favor it over the chance hypothesis at best only very weakly, because evidence is conventionally regarded as worth considering only when the absolute value of the weight of the evidence is greater than .5 (meaning that Bayes Factor > 3 or < .33).
These weigh against the simplest form of the clairvoyance hypothesis (.5 ≤ p ≤ 1), because it makes a lot of bad bets. They weigh slightly in favor of the hedged forms, because they place their chips more astutely. Mostly, though, we see that these data do not substantially favor any one of our clairvoyance hypotheses over any of the others or over the null. Importantly, however, the data could strongly favor the null hypothesis over any formulation of the clairvoyance hypothesis that was nontrivially different from the null. They would do so if, for example, she made 490 successful predictions in 1000 flips, an entirely plausible result if she is just guessing.



Comments
It is possible the lower figure in Fig. 1 is only an approximation (i.e. it’s the graph obtained from calculating the Bayes Factor for x=0.6 [0.5<= rho <= 0.6], x=0.7, x=0.8, x=0.9 and x=10)?
When I ran a similar graph for 51 hyphotesis:
H_0.5: rho = 0.5
H_0.51: 0.5<= rho <= 0.51
H_0.52: 0.5<= rho <= 0.52
….
H_1: 0.5<= rho <= 1
the shape is much more rounded, and in particular there is not a flat region between 0.6 and 0.7
APS regularly opens certain online articles for discussion on our website. Effective February 2021, you must be a logged-in APS member to post comments. By posting a comment, you agree to our Community Guidelines and the display of your profile information, including your name and affiliation. Any opinions, findings, conclusions, or recommendations present in article comments are those of the writers and do not necessarily reflect the views of APS or the article’s author. For more information, please see our Community Guidelines.
Please login with your APS account to comment.